平衡二叉树的定义:
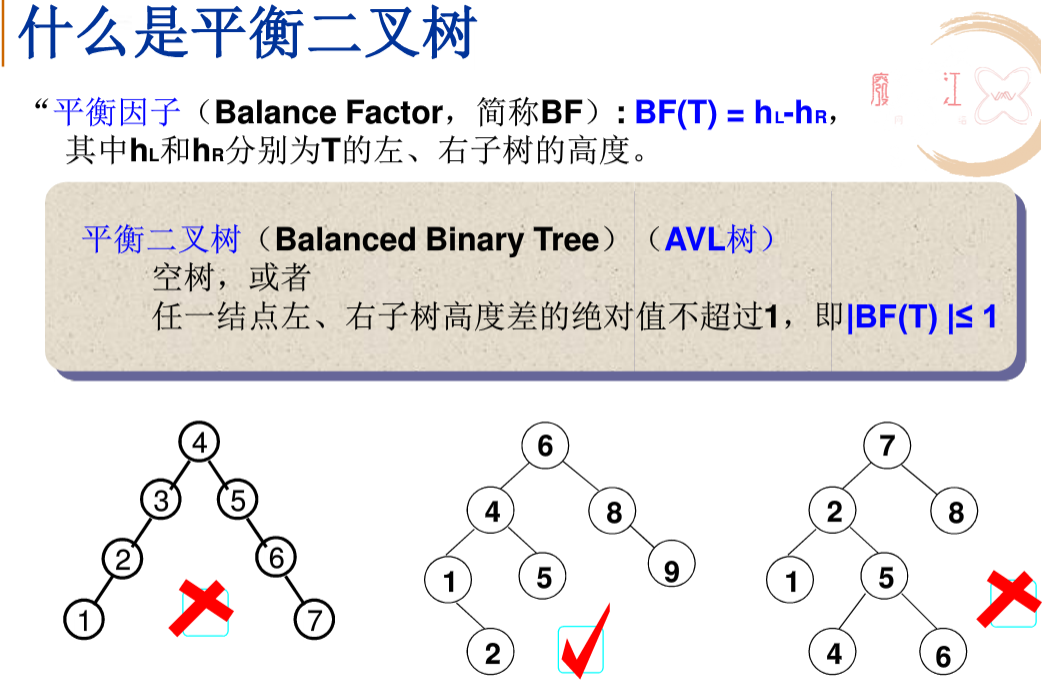
结论:给定节点数为n的avl树的最大高度为0(log2n)
平衡二叉树的调整:rr旋转,ll旋转,lr旋转和rl旋转
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
typedef struct AVLNode *Position; typedef Position AVLTree; /* AVL树类型 */ struct AVLNode{ ElementType Data; /* 结点数据 */ AVLTree Left; /* 指向左子树 */ AVLTree Right; /* 指向右子树 */ int Height; /* 树高 */ }; int Max ( int a, int b ) { return a > b ? a : b; } AVLTree SingleLeftRotation ( AVLTree A ) { /* 注意:A必须有一个左子结点B */ /* 将A与B做左单旋,更新A与B的高度,返回新的根结点B */ AVLTree B = A->Left; A->Left = B->Right; B->Right = A; A->Height = Max( GetHeight(A->Left), GetHeight(A->Right) ) + 1; B->Height = Max( GetHeight(B->Left), A->Height ) + 1; return B; } AVLTree DoubleLeftRightRotation ( AVLTree A ) { /* 注意:A必须有一个左子结点B,且B必须有一个右子结点C */ /* 将A、B与C做两次单旋,返回新的根结点C */ /* 将B与C做右单旋,C被返回 */ A->Left = SingleRightRotation(A->Left); /* 将A与C做左单旋,C被返回 */ return SingleLeftRotation(A); } /*************************************/ /* 对称的右单旋与右-左双旋请自己实现 */ /*************************************/ AVLTree Insert( AVLTree T, ElementType X ) { /* 将X插入AVL树T中,并且返回调整后的AVL树 */ if ( !T ) { /* 若插入空树,则新建包含一个结点的树 */ T = (AVLTree)malloc(sizeof(struct AVLNode)); T->Data = X; T->Height = 0; T->Left = T->Right = NULL; } /* if (插入空树) 结束 */ else if ( X < T->Data ) { /* 插入T的左子树 */ T->Left = Insert( T->Left, X); /* 如果需要左旋 */ if ( GetHeight(T->Left)-GetHeight(T->Right) == 2 ) if ( X < T->Left->Data ) T = SingleLeftRotation(T); /* 左单旋 */ else T = DoubleLeftRightRotation(T); /* 左-右双旋 */ } /* else if (插入左子树) 结束 */ else if ( X > T->Data ) { /* 插入T的右子树 */ T->Right = Insert( T->Right, X ); /* 如果需要右旋 */ if ( GetHeight(T->Left)-GetHeight(T->Right) == -2 ) if ( X > T->Right->Data ) T = SingleRightRotation(T); /* 右单旋 */ else T = DoubleRightLeftRotation(T); /* 右-左双旋 */ } /* else if (插入右子树) 结束 */ /* else X == T->Data,无须插入 */ /* 别忘了更新树高 */ T->Height = Max( GetHeight(T->Left), GetHeight(T->Right) ) + 1; return T; } |

