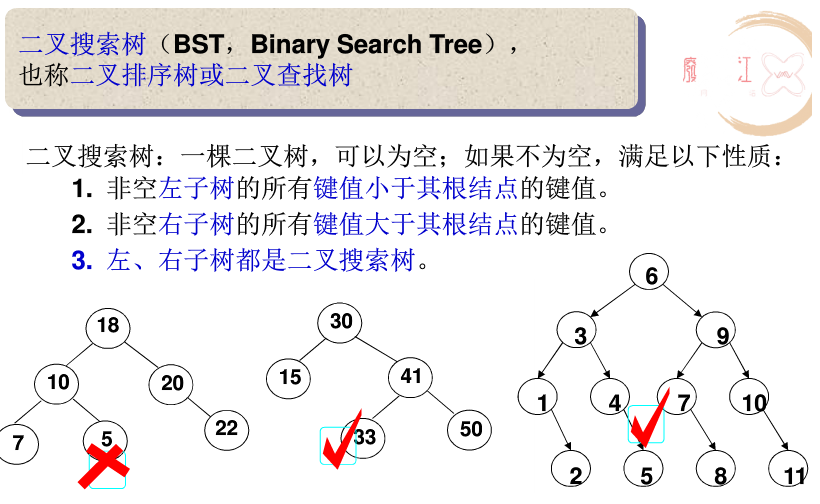
搜索二叉树的定义很简单:
![7ebb2688f0ec88d901ab162252765e60.png]()
搜索二叉树可以用中序遍历来实现排序输出。。。
下面是自己写的搜索二叉树的代码
搜索二叉树可以用中序遍历来实现排序输出。。。
下面是自己写的搜索二叉树的代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
#include<bits/stdc++.h> using namespace std; typedef int ElementType ; typedef struct tnode *BinTree; typedef BinTree Position ; struct tnode { ElementType Data; BinTree Left; BinTree Right; }; Position FindMin( BinTree BST){ if (!BST) return NULL; else if (!BST->Left) return BST; else return FindMin(BST->Left); } Position FindMax( BinTree BST){ if(BST) while ( BST->Right) BST =BST->Right; return BST; } BinTree Insert( BinTree BST, ElementType X ) { if( !BST ) { BST = (BinTree)malloc(sizeof(struct tnode)); BST->Data = X; BST->Left = BST->Right = NULL; } else { if( X < BST->Data ) BST->Left = Insert( BST->Left, X ); else if( X > BST->Data ) BST->Right = Insert( BST->Right, X ); } return BST; } BinTree Delete( BinTree BST, ElementType X ) { Position Tmp; if( !BST ) printf("要删除的元素未找到"); else { if( X < BST->Data ) BST->Left = Delete( BST->Left, X ); /* 从左子树递归删除 */ else if( X > BST->Data ) BST->Right = Delete( BST->Right, X ); /* 从右子树递归删除 */ else { /* BST就是要删除的结点 */ /* 如果被删除结点有左右两个子结点 */ if( BST->Left && BST->Right ) { /* 从右子树中找最小的元素填充删除结点 */ Tmp = FindMin( BST->Right ); BST->Data = Tmp->Data; /* 从右子树中删除最小元素 */ BST->Right = Delete( BST->Right, BST->Data ); } else { /* 被删除结点有一个或无子结点 */ Tmp = BST; if( !BST->Left ) /* 只有右孩子或无子结点 */ BST = BST->Right; else /* 只有左孩子 */ BST = BST->Left; free( Tmp ); } } } return BST; } BinTree Find( BinTree BST, ElementType X ) { if(!BST ) return NULL; if( X >BST->Data ) return Find(BST->Right,X); else if(X<BST->Data) return Find(BST->Left,X); else return BST; } void preorder(BinTree BST){ //先序遍历 if(BST){ printf("%d ",BST->Data); preorder(BST->Left); preorder(BST->Right); } } void inorder(BinTree BST){ //中序遍历 if(BST){ inorder(BST->Left); printf("%d ",BST->Data); inorder(BST->Right); } } int main() { BinTree BST; BST=NULL; // int a[10]; // for(int i=0;i<9;i++) // cin>>a[i]; // for(int i=0;i<9;i++){ // BST=Insert(BST,a[i]); // } for(int i=0;i<9;i++){ BST=Insert(BST,i); } preorder(BST); cout<<endl; inorder(BST); } |

